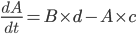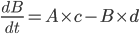The Beth Project

Journal Club: How Anti-Arrhythmic Drugs Increase the Rate of Sudden Cardiac Death

We had the first meeting of our cardiac modelling journal club yesterday, and we looked at this paper by C. Frank Starmer from 2002.

The paper was investigating "Sanderson's paradox", whereby drugs intended to treat cardiac arrhythmia actually increased the incidence of sudden cardiac death in patients, even though they displayed what were thought to be anti-arrhythmic properties in single cells. (Incidentally, I think "paradox" is an overly dramatic word for "we discovered that we were wrong about something"). He was looking specifically at sodium blockers, because they were common anti-arrhythmic drugs.

He first describes a method for modelling drug block: it has been observed that sodium blockers are more effective when the heart is paced faster. This would suggest that the drug might bind only to the open ion channel. He formulated this as an extra gate on the sodium channel in addition to the h, m, and j gates.

He next talks about the refractory interval, which is the length of time a cell spends being unable to depolarise again after the initial stimulus. It was generally considered that increasing the refractory interval would be anti-arrhythmic, because it would make the cell less vulnerable to being stimulated by some random event.
So the thought was that you'd start with this:

And then your drug would change it to this:

Judging by the results of these drugs in humans, however, it looks like this isn't what happens on a larger scale. Starmer then looked at a group of cells arranged in a 1-dimensional cable, and talked about finding a different definition for the vulnerable period, based on the properties of the whole cable.

Usually when you apply an electrical stimulus (S1) (like you'd get during a heartbeat) to the end of a 1D cable, like so:

You get a wave propagating away from the stimulus, as expected:

This is all fine and normal, but what if you had a second stimulus (S2) outside of the usual time and place of stimulation?

You'd either get a wave propagating backwards along the cable:

or waves going in both directions:

In 1D, having an aberrant wave that propagates in one direction only is a pro-arrhythmic marker, because it could lead to a re-entrant arrhythmia in the whole heart. It's important, therefore, to work out what amount of drug block is going to cause unidirectional propagation and what amount bidirectional, and to redefine the "vulnerable period" as a property of the propagating wave. The vulnerable period depends on such things as the distance and time between S1 and S2, the speed of the wave, and the sodium channel availability.

If I have understood this paper correctly, the vulnerable region is the time between there being enough sodium channel availability at the location of S2 to create a backwards wave and there being enough availabiltity to create a forwards wave at the same location.

This was a really interesting thing to do, and I'm looking forward to having more journal club sessions, because it helped me to pick out the parts of the paper that I thought I understood but didn't, and brought together a lot of clever people in a room to explain them to me.

Gedit add-ons for LaTeX

The default text editor that comes with the Gnome GNU/Linux desktop is called gedit, and I like using it for editing LaTeX and HTML. I have a few little tweaks I use for a smoother user experience.

Firstly, I can use it as an easy file browser, by going to View > Side Panel, and then clicking on the filing cabinet at the bottom of the panel.

Secondly, gedit has the option of adding little shell scripts that you can set to execute using a keyboard shortcut, by going to Tools > Manage External Tools. I have three useful scripts that I can run on a LaTeX document that I'm currently editing.

Ctrl+Q: TeXCount. Count the number of words in the document, ignoring markup.


#!/bin/sh
NUMWORDS=$(texcount $GEDIT_CURRENT_DOCUMENT_NAME)
exec `zenity --info --title="TeXCount output" --text="$NUMWORDS"`

Ctrl+Alt+W: BibTeX. Insert references into the document.


#!/bin/sh
FULLNAME=$GEDIT_CURRENT_DOCUMENT_NAME
SHORTNAME=${FULLNAME%.tex}
bibtex $SHORTNAME

Ctrl+Alt+Q: PDFLaTeX. Compile the document into a PDF.


#!/bin/sh
pdflatex $GEDIT_CURRENT_DOCUMENT_NAME

I've also had to play around with bibliography styles a bit lately. I've slightly modified the usual abbrv.bst and abbrvnat.bst bibliography style files (which are usually this and this), to stop them from displaying the month:

no-month.bst
no-monthnat.bst

To use, just download the file and put it in the same directory as your document, and then put either:

\bibliographystyle{no-month}

\bibliographystyle{no-monthnat}

in the markup.

I'm really glad I get to use LaTeX for everything. It can be a bit of a struggle to enact specific changes to the formatting, but in general it's easy to get a beautiful document while enjoying the portability and robustness of simple text files.

NC3Rs workshop

The main motivation behind my research is coming up with new and better methods for testing drugs and other substances to see if they are effective and safe. I've written previously about some of the promising animal testing alternatives that are being created.

Last week I went to a workshop run by the national centre for the replacement/refinement/reduction of animals in research (NC3Rs) and POEMS. Biologists brought 3Rs problems, and a group of computational and mathematical modellers tried to solve them.

There were five different projects presented. One was about using fruit flies to model diseases like Alzheimer's and Parkinson's by seeing how their courting behaviour is affected, another was modelling the way that nerves respond to bladder filling, one was related to immunoglobulin, and another was modelling retina damage in shaken baby syndrome (so much respect for the people who picked that project. It's really important but heartbreaking). The project I chose was about testing for neurodevelopmental safety.

The problem

If you affect the amount of thyroid hormones in the body of a pregnant woman, it can have huge effects on the developing foetus. A lot of potential drugs, potential industrial chemicals and potential pesticides turn out to significantly reduce the amount of thyroid hormones in the blood, meaning that they aren't safe to use around people.

Currently if you want to bring a new chemical to market, you have to test for thyroid effects using about 40 pregnant rats, each of which could be pregnant with up to 10 pups. We wanted to see if it was possible to use data from earlier studies on a few adult male rats to predict these effects, without having to use any extra animals. This method would still use data from animal tests, but would reduce the number of animals used, and could pave the way towards a non-animal method later on.

The picture below shows a simplified version of the pathway that thyroid hormones take through the body. T4 is produced in the mother's thyroid gland and then secreted into her blood. From here, it can either be removed by the liver, or carried into the blood of her foetus. It then travels from the foetus' blood to its developing brain cells. Inside the brain cells, T4 is converted into T3, which is essential for the brain to develop correctly (for a review, see Williams, 2008).

We concentrated on modelling the last two steps of this pathway: the transport of T4 from the outside of the cell to the inside, and its conversion to T3. The amount of T3 that ends up bound to its receptor in the nucleus is the most important variable for brain development. We wanted to see how the concentration of T4 in the foetus' blood affected the concentration of receptor-bound T3 in the nucleus.

The process

First, we all sat down together and came up with a set of equations to describe the way that all the components of the regulatory network interacted with each other. We used simple ordinary differential equations, which you might recognise from chemistry lessons.

For example, if a molecule A turns into a different molecule B at a rate of c molecules per second, and B turns into A at a rate of d molecules per second, you can say that

and

This way, given starting concentrations for A and B, you can work out how many molecules of each you have at a given time. We used this method to write down equations to describe the whole network.

After this, we each followed a different path of investigation. One researcher tried to derive analytically an equation to describe what steady state the system will reach, while others performed sensitivity analysis and parameter fitting. I was in a group that were looking at Petri nets, which are a different way of describing reaction networks, with some useful tools for analysis.

An animation of the petri net for this system is shown below. The circles (known as "places"), represent possible states that molecules can be in, the numbers inside the places represent the number of molecules in that state. The squares are transitions - usually representing some kind of reaction or binding event - and the red dots moving between places and transitions are the molecules as they change from place to place.

Petri nets seem like a really useful way of modelling biological systems for people without much experience of ODEs or programming, because they are a direct analogue for a system of ODEs with all the rate constants set to 1. The next stage in our analysis will be to parameterise this model, and use some graph theory tools to find out new things about the system. I haven't done graph theory since A-level, so this should be quite interesting!