The latte millionaire fallacy

Edit: This got picked up by the New York Post - hi to everybody who clicked through from there.

coffee-922914_640

An idea oft floated around the internet is: "if you avoid buying your daily latte and instead put the money in a savings account, you could be a millionaire by the time you retire." I think it was the book "The Automatic Millionaire" by David Bach that first popularised the idea.

I'm not going to argue that it's not worth saving money on non-essentials (although if you're in dire financial straits you probably don't need to be told this - contrary to some oddly popular rhetoric, people with low incomes do tend to also spend less money, especially if they are unemployed).

What bothers me is that, at realistic interest rates, you're very unlikely to make it to a million pounds. You'd save a lot of money, but you'd be far short.

Other people have also written about this, but I thought I'd quickly break down the maths.

Say you spend x pounds on a latte every day (in reality, probably around £3). Instead of buying this latte, you decide to invest the money in a savings account with an interest rate of y (probably between 3-6%). After n years, you will have £T.

So how do we work this out?

At the end of the first year, you put in £x.

T_1 = 365.25 x

In the second year, you'll get the first amount with interest, plus all the money you've added in the second year.

(Sidenote: I'm using a multiple for the interest, e.g. 3% interest is expressed as 1.03)

T_2 = 365.25 x y + 365.25 x

The next year, you get all of that money with interest, plus your new deposits.

T_3 = (365.25 x y + 365.25 x) y + 365.25 x

This could also be expressed as:

T_3 = 365.25 x y^2 + 365.25 x y + 365.25 x

This is looking like a geometric series, yay! If we come up with a generic expression for the total amount, it looks like this:

T_n = 365.25 x y^{n-1} + 365.25 x y^{n-2} + ... + 365.25 x y + 365.25 x

Now, if you can remember your GCSE maths, the way we find out the sum of a geometric series is by multiplying it by y:

T_n y = 365.25 x y^{n} + 365.25 x y^{n-1} + ... + 365.25 x y^2 + 365.25 x y

and then taking it away so you can cancel out most of the terms:

T_n - T_n y = 365.25 x - 365.25 x y^n

Now let's get all the T_ns on one side of the equation, and everything else on the other side:

T_n (1 - y) = 365.25 x (1 - y^n)

T_n = \frac{365.25 x (1 - y^n)}{1 - y}

So if you invest your £3 per day latte money into an account paying 6% interest for 50 years, you'll end up with:

T_{50} = \frac {365.25 \times 3 (1 - 1.06^{50})}{1 - 1.06}

T_{50} = \pounds 318,135.57

Don't get me wrong, £318,135.57 is not chump change, but it's less than a third of the way to a million.

In fact, if you wanted a million pounds from a £3 latte habit, you'd need an interest rate of 9.6%. At an interest rate of 6%, your latte would have to cost £9.43.

Here are all the likely interest rates and latte cost combinations that will net you a million pounds by this method:

Minimum interest and cost combination required to accumulate a million pounds
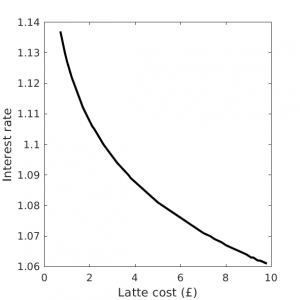
Interest rate - latte cost combinations required for millionaire-dom

As you can see, you'd require a very high interest rate or a very expensive latte.

Again, I'm not against saving money and making your coffee at home; I'm against the propagation of inaccurate mathematics.

XKCD cartoon about compound interest
As always, XKCD said it best.

Addenda:

  1. I was thinking about inflation, but decided that there were too many factors to consider (your money would be worth less at the end, but also your latte would cost more and perhaps your interest rate would rise...)
  2. Several people have mentioned that it's likely that people would only buy their latte on the way to work for 5 days a week. They'd also have some holiday days during the year. Considering how much shift work, zero-hours contracts, overtime, and working multiple jobs that people do, calculating these factors made my head hurt, so I choose instead to believe that these people go out on the weekends for a latte at the nice artisan café down the road.
  3. It has also been pointed out that finding a bank account with a 6% rate of interest is nigh-on impossible. If I've interpreted the maths correctly, this means that you won't become a millionaire unless you start buying a more expensive latte.

If you'd like to get email updates from me, sign up to my mailing list!

...

10 thoughts on “The latte millionaire fallacy”

  2. Million is probably a stretch, but the pursuit of being conscious about expenditures and instead saving is likely to be worthwhile anyway. I know you are not arguing this point, but catchy titles for a book and the lure of a "million" is probably what draws people in and gets them to do *something* even if it isn't the full amount stated that drew them in. People need to feel that what they're doing is making an impact.

    Also, the assumption of the asset class they chose - a savings account, may not be the best. For retirement, you have a long term liability and a short term instrument like a savings account is mismatched. You are better off buying equities (whether domestic or international, or a mix ideally) that should produce a higher return through both dividends and index growth over time. Hopefully, this brings us closer to that "million" amount. If you do the equity route, remember to buy broad indices with low fees and to dollar cost average over time!

    Reply

    2. The idea behind that principle is not that you park the savings in a CD or savings account... it's that you invest it in the stock market. Your math doesn't account for investing those saved funds in something like an ETF or growth stock mutual fund.

      Reply

    3. It does not, in fact, bring us closer to that 'million' amount. Long-term (VERY) stocks average almost exactly 7%, not much different than the 6% assumed above. And that does not take into account the risks of, for example, cutting off your latte habit in 1960 and retiring in 1985, resulting in a growth net of inflation of about 0%.

      Reply

  3. Thanks. I feel less guilty now when drinking my €3 lattés.

    Another oft-quoted maxim: Lattés will not bankrupt you; cost of healthcare will.

    Reply

    1. That wasn't actually the aim of the article! I mean, you do you, but my point is that it's an oversimplification based on incorrect mathematics.

      I'm with you on the healthcare, though >.<

      Reply

  4. Her Future Value (FV) calculation is wrong. In order to get the FV of 318, 135.57 she lumps all 3 daily payments into one yearly payment of 1095.75.

    On a financial calculator:

    n 50
    i 6
    PV 0
    PMT 1095.75
    FV ?

    FV = 318,135.57

    This is incorrect. The payments are not once a year, they are daily (or equivalently, they are daily swipes of your bank card that are **not** swiped at the coffee shop). So you're earning compound interested *each day* on the total deposits thus far. You also need to adjust the interest rate for the compounding period.

    Again, a financial calculator will make this much easier.

    n 365.25x50
    i 6/365.25
    PV 0
    PMT 3
    FV ?

    FV = 348,429.14

    If you do not have a financial calculator ... GO BUY ONE.

    Until it arrives, you will need the equivalent annual rate (EAR):

    EAR = (1 + periodic interest rate)^*m* - 1

    There's more to this, such as the tax favored investing available via 401k plans (as mentioned by others in this thread) but I'm on mobile and my finger is getting sore.

    Reply

  5. The takeaway is: Changing daily habits such as making your own coffee or buying cheaper brands CAN monumentally change your long term financial position.

    Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

*

CAPTCHA

*

This site uses Akismet to reduce spam. Learn how your comment data is processed.