Category: Journal Club

Monday's journal club was on this Wang et al. 1997 paper. They took the hERG gene, which was thought to be responsible for the rapid delayed rectifier potassium current in humans, and put it into unfertilised frog eggs, then used patch clamping to find out its properties.

I think a lot about how the membrane potential is affected by the currents that are flowing across it, but sometimes it is good to remember that the currents themselves are modified by the membrane voltage. In cardiac models, the currents tend to be modelled as:

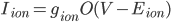
where 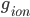is the conductance, 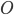is the proportion of channels that are active, 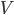is the membrane voltage, and 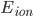the reversal potential. 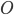is often affected by the membrane potential, as well, so the membrane voltage plays a key role in regulating current flow.

Usually, the voltage across the membrane of a cardiac cell looks a bit like this:

If we're doing a patch clamp then we stick an electrode to the outside of the cell, which means that we can control what the membrane potential does. We could make it do this:

... or use the same shape, but don't bring the voltage up as far:

In the case of hERG, this lets us see what happens when the current is activated, because hERG switches on at high voltages. By comparing the activation time at lots of different potential steps, you can begin to understand the activation kinetics of the channel. In this paper, they were able to put together a model of what happens, by taking models with various numbers of closed states and comparing their predictions to the real data.

Activation kinetics are important, but so are deactivation kinetics. The hERG channels close when the membrane potential decreases, so if we activate them and then let the voltage drop down again, we should be able to see what happens when they close:

Again, we can try lots of different voltages:

... and from this, build up a model of the deactivation of this current. Inactivation (which is distinct from deactivation, because it stops the channels from being openable for a period of time) happens very quickly, so they had to cut open the cells for their patch clamp. I'd never come across this method before, but I came across quite a good review article.

In addition to creating a mathematical model of this current, the authors also talk a little bit about possible molecular reasons for the behaviour of the channel. This isn't something I've seen a lot in electrophysiology modelling papers, and I think it's really important to keep an eye on the fact that in addition to being a model component, what we're modelling is a real, physical protein, and mechanistic understanding of how that works can feed back into modelling work.

We had the first meeting of our cardiac modelling journal club yesterday, and we looked at this paper by C. Frank Starmer from 2002.

The paper was investigating "Sanderson's paradox", whereby drugs intended to treat cardiac arrhythmia actually increased the incidence of sudden cardiac death in patients, even though they displayed what were thought to be anti-arrhythmic properties in single cells. (Incidentally, I think "paradox" is an overly dramatic word for "we discovered that we were wrong about something"). He was looking specifically at sodium blockers, because they were common anti-arrhythmic drugs.

He first describes a method for modelling drug block: it has been observed that sodium blockers are more effective when the heart is paced faster. This would suggest that the drug might bind only to the open ion channel. He formulated this as an extra gate on the sodium channel in addition to the h, m, and j gates.

He next talks about the refractory interval, which is the length of time a cell spends being unable to depolarise again after the initial stimulus. It was generally considered that increasing the refractory interval would be anti-arrhythmic, because it would make the cell less vulnerable to being stimulated by some random event.
So the thought was that you'd start with this:

And then your drug would change it to this:

Judging by the results of these drugs in humans, however, it looks like this isn't what happens on a larger scale. Starmer then looked at a group of cells arranged in a 1-dimensional cable, and talked about finding a different definition for the vulnerable period, based on the properties of the whole cable.

Usually when you apply an electrical stimulus (S1) (like you'd get during a heartbeat) to the end of a 1D cable, like so:

You get a wave propagating away from the stimulus, as expected:



This is all fine and normal, but what if you had a second stimulus (S2) outside of the usual time and place of stimulation?



You'd either get a wave propagating backwards along the cable:



or waves going in both directions:



In 1D, having an aberrant wave that propagates in one direction only is a pro-arrhythmic marker, because it could lead to a re-entrant arrhythmia in the whole heart. It's important, therefore, to work out what amount of drug block is going to cause unidirectional propagation and what amount bidirectional, and to redefine the "vulnerable period" as a property of the propagating wave. The vulnerable period depends on such things as the distance and time between S1 and S2, the speed of the wave, and the sodium channel availability.

If I have understood this paper correctly, the vulnerable region is the time between there being enough sodium channel availability at the location of S2 to create a backwards wave and there being enough availabiltity to create a forwards wave at the same location.

This was a really interesting thing to do, and I'm looking forward to having more journal club sessions, because it helped me to pick out the parts of the paper that I thought I understood but didn't, and brought together a lot of clever people in a room to explain them to me.