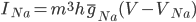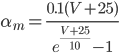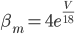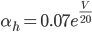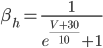Further to my last post, in which I attempt to form a vague understanding of Hodgkin and Huxley's giant squid axon model, I'm now looking at the gating mechanisms they used.
The opening, closing and inactivation of ion channels is vital for the characteristic shape of the action potential.
A) The sodium channels open and sodium floods into the cell: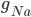 
increases.
B) The potassium channels open, allowing potassium out of the cell: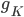 
increases.
C) The sodium channels are inactivated when the membrane voltage is at its highest: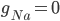 
.
D) The potassium channels close and the sodium channels are activated when the membrane voltage reaches its lowest: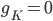 
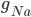and increases.
This means that the sodium and potassium conductances vary in a complicated way with changes in the membrane voltage. The 'leak' current is simply directly proportional to the membrane voltage.
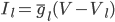
The changes in conductivity are modelled as "gates" for the sodium and potassium channels. The gates are represented by a dimensionless variable, which can be between 1 (fully active) and 0 (fully inactive). The rate of change of a gate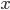 
with time is defined as:
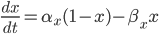
where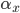 
is the rate of movement of ions from outside to inside, and 
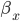is the reverse.
Unlike for the rest of the model's features, the gating of the ion channels is not worked out from first principles. Instead, equations were fitted to match empirical data from experiments. Hodgkin & Huxley took measurements of each ionic current while keeping the membrane voltage constant, over a variety of different voltages, and used the data to find 
and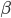 
expressions for each gate as functions of voltage.
For the potassium channel, there is only one type of gate, called the "n" gate. The permeability of the membrane to potassium varies with the 4th power of n (for equation fitting-ey reasons).
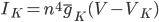
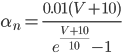
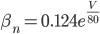
For the sodium channels, there are two types of gate. The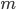 
gate being active encourages flow of sodium ions through the membrane, but the 
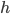gate being active inactivates the sodium channels.
