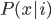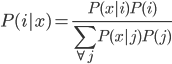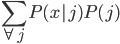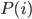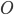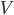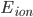Category: Science

Installing Chaste on Debian (sorta)

For my research, I program using a collossal C++ software package called "Chaste". CHASTE stands in this case for "Cancer, Heart and Soft Tissue Environment", rather than its usual meaning of the sexual repression of people (especially women) all over the world. Interesting choice of acronym.

Chaste's got lots and lots of bits that I don't use, and it is notoriously difficult to install on things, but it's also incredibly, incredibly useful. Over the last 10 years or so people have added all kinds of modules for biological modelling, especially cardiac stuff. Just a quick look at the class index gives you an idea of how many tools there are to use.

There's an easy Chaste installer for Ubuntu, but I'm a Debian girl myself, and I've had terrible trouble trying to use the generic instructions, because there are a lot of dependencies, and each dependency has different versions in different Linux distributions.

In the end, I decided to side-step the issue entirely. There's a tool called Debootstrap, which creates an entire Ubuntu installation in a single folder, so I can be using my Debian laptop and have Ubuntu open in a terminal without too much bother.

So first we make a Chaste directory and put Ubuntu into it using debootstrap:

mkdir Chaste
sudo debootstrap utopic Chaste http://mirrors.kernel.org/ubuntu/dists/utopic/

Next, we jump into the Ubuntu installation by changing our root:

sudo chroot Chaste

First off for some reason you need to tell the computer where you are.

locale-gen en_GB en_GB.UTF-8

Then there are a few useful things that I like to have around; "nano", which is a text editor, "aptitude" which is a front-end for the apt-get installer, and "man" which are the manual pages for command line tools.

apt-get install nano aptitude man

Now you need to add some more repositories so that you have all of the packages available that you need. Open up your sources file:

nano /etc/apt/sources.list

Delete the first line using Ctrl-K, and then copy in the following:

deb http://archive.ubuntu.com/ubuntu utopic main universe multiverse
deb http://archive.canonical.com/ubuntu utopic partner
deb http://archive.ubuntu.com/ubuntu utopic-backports main restricted universe multiverse
deb-src http://us.archive.ubuntu.com/ubuntu/ utopic universe main multiverse
deb http://us.archive.ubuntu.com/ubuntu/ utopic-updates universe multiverse
deb-src http://us.archive.ubuntu.com/ubuntu/ utopic-updates universe multiverse
deb http://www.cs.ox.ac.uk/chaste/ubuntu utopic/

Then press Ctrl-O to save and Ctrl-X to exit. Next, we add the Chaste license key, and update the package lists.

apt-key adv --recv-keys --keyserver hkp://keyserver.ubuntu.com:80 422C4D99
apt-get update

The proc filesystem needs to be mounted before we can continue:

mount -t proc proc /proc

After this point, I am just following the default install guide. This next part took forever, I got quite bored. Here is a collection of margin scribbles from books.

apt-get install --install-recommends chaste-dependencies
apt-get install `dpkg -s chaste-dependencies | egrep "^Suggests" | cut -d "," -f 1-111 --output-delimiter " " | cut -d ":" -f 2`

Then checkout the code! I put it into a folder called "Chaste" in the root directory, but if you want to put it somewhere else (/home/scratch/Chaste/ for example) just create the directory you need first and cd into it.

svn --username anonymous checkout https://chaste.cs.ox.ac.uk/svn/chaste/trunk/ Chaste
cd Chaste
scons

Then all of the tests should start building!

...

Playing with Linear Discriminant Analysis

The way that I select which risk category a drug should be in based on the training data I have is called Linear Discriminant Analysis (LDA). I've made a little example of how it works using MATLAB (however, this code also works perfectly on the wonderful, and free, Octave).

You can download my MATLAB/Octave script and try it out yourself (it takes one input, a number). Below, I'll go through it step by step.

function LDA(point)

%% group 1: mean 10, sd 2
%% group 2: mean 3, sd 1
%% group 3: mean 5, sd 0.5

group_1 = 10 + 2*randn(10,1);
group_2 = 3 + randn(10,1);
group_3 = 5 + 0.5*randn(10,1);

These first few lines create a set of training data, by making random numbers based on three normal distributions with different means and standard deviations. In real life, you wouldn't know how your data were generated or what distribution they came from. 

%% plot all of the training data
hold off
plot(group_1, zeros(10,1),'o')
hold on
plot(group_2, zeros(10,1),'+')
plot(group_3, zeros(10,1),'.')

Now for visualisation we plot the training data, delineating the different groups by differently shaped markers.

%% find the likelihood of the point given the group
p_x1 = normpdf(point,mean(group_1),std(group_1));
p_x2 = normpdf(point,mean(group_2),std(group_2));
p_x3 = normpdf(point,mean(group_3),std(group_3));

The first thing we need to find is the probability that this point (the input number, in this case 9.5114) would exist given the group that it's a member of, i.e. . In LDA, you assume that the points within each group are normally distributed, so in MATLAB/Octave there's a useful function called normpdf that calculates the probability of a point given the mean and standard deviation of the distribution.

%% find the probability of the group given the point using Bayes' rule
p_i1 = (p_x1*(1/3))/((p_x1+p_x2+p_x3)*1/3);
p_i2 = (p_x2*(1/3))/((p_x1+p_x2+p_x3)*1/3);
p_i3 = (p_x3*(1/3))/((p_x1+p_x2+p_x3)*1/3);

Bayes' rule is that .

is actually the same for all groups, so we can ignore it. Because there are three groups of ten items, we know that is always . This means that we could have simplified these calculations by just comparing the likelihoods (). 

%% which one has the maximum probability?
[a b] = max([p_i1,p_i2,p_i3]);

if b==1
    dotshape = 'o';
elseif b==2
    dotshape = '+';
else
    dotshape = '.';
end

%% plot to see if we're right
plot(point,0,strcat(dotshape,'r'))
hold off

end

We end by picking the group that has the highest probability, i.e. the highest , and then plot that on the graph.

If you have more than one set of data points (i.e. if you are classifying based on two features), you can assume that the covariances in different groups are all equal, which simplifies the calculations for that system.

...

Journal Club: a Quantitative Analysis of the Activation and Inactivation Kinetics of HERG Expressed in Xenopus Oocytes

Monday's journal club was on this Wang et al. 1997 paper. They took the hERG gene, which was thought to be responsible for the rapid delayed rectifier potassium current in humans, and put it into unfertilised frog eggs, then used patch clamping to find out its properties.

I think a lot about how the membrane potential is affected by the currents that are flowing across it, but sometimes it is good to remember that the currents themselves are modified by the membrane voltage. In cardiac models, the currents tend to be modelled as:

where is the conductance, is the proportion of channels that are active, is the membrane voltage, and the reversal potential. is often affected by the membrane potential, as well, so the membrane voltage plays a key role in regulating current flow.

Usually, the voltage across the membrane of a cardiac cell looks a bit like this:



If we're doing a patch clamp then we stick an electrode to the outside of the cell, which means that we can control what the membrane potential does. We could make it do this:



... or use the same shape, but don't bring the voltage up as far:



In the case of hERG, this lets us see what happens when the current is activated, because hERG switches on at high voltages. By comparing the activation time at lots of different potential steps, you can begin to understand the activation kinetics of the channel. In this paper, they were able to put together a model of what happens, by taking models with various numbers of closed states and comparing their predictions to the real data.

Activation kinetics are important, but so are deactivation kinetics. The hERG channels close when the membrane potential decreases, so if we activate them and then let the voltage drop down again, we should be able to see what happens when they close:



Again, we can try lots of different voltages:



... and from this, build up a model of the deactivation of this current. Inactivation (which is distinct from deactivation, because it stops the channels from being openable for a period of time) happens very quickly, so they had to cut open the cells for their patch clamp. I'd never come across this method before, but I came across quite a good review article.

In addition to creating a mathematical model of this current, the authors also talk a little bit about possible molecular reasons for the behaviour of the channel. This isn't something I've seen a lot in electrophysiology modelling papers, and I think it's really important to keep an eye on the fact that in addition to being a model component, what we're modelling is a real, physical protein, and mechanistic understanding of how that works can feed back into modelling work.

...