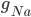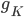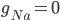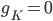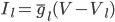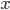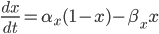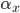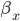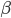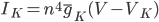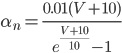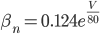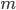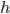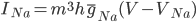Category: Geeking

I've spent the last few weeks (amongst other things) implementing my afterdepolarisations script in C++ within the Chaste framework. Here's some of my code broken down into sections and explained.

#include "DetectAfterDepolarisations.hpp"
#include <fstream>

bool DetectAfterDepolarisations::FindAD(std::vector<double> voltage, std::vector<double> simtimes,
    double end_time, double stim_start, double stim_period, double lowlimit, double highlimit)
{

This function takes as inputs: a vector containing the voltage trace for every time point, a vector of all the times, the end time of the simulation, the time at which the stimulus starts, the period of the stimulus, and the two boundary values for detection. It will output either "true", if there is an afterdepolarisation, or "false", if not.

    /* detect depolarisations*/
    std::vector<double> differences;
    std::vector<double> adtimes;
    for (unsigned int a=0; a < voltage.size()-1; a++)
    {
        /* list of voltage change at each time point*/
        differences.push_back(voltage[a+1]-voltage[a]);
        /* if the voltage is going up... */
        if (differences[a] > 0.1)
            /* store the time */
            adtimes.push_back(simtimes[a]);
    }

The way this works isn't desperately clever: it takes each point on the graph and subtracts it from the one after it, giving the gradient between each point. For all the positive changes in voltage (arbitrarily those over 0.1 mV), it keeps a note of the time.

    /* erase depolarisations provoked by stimulus */
    for (double e = stim_start; e < end_time; e=e+stim_period)
    {

        for (unsigned int f=0; f<adtimes.size(); f++)
        {

            if (adtimes[f] > e-lowlimit && adtimes[f] < e+highlimit)
            {

                adtimes.erase(adtimes.begin()+f);
                f--;
            }
        }

    }

These awkwardly nested loops check all of the depolarisation times and remove any that coincide with the stimulus. This means that the program finds only afterdepolarisations and not the ones we'd expect to be there. Lowlimit and highlimit can be changed for models with different lengths of action potential.

    /* find times when the AD starts */
    std::vector<double> diffadtimes;

    /* iterate through list of voltage upswing times*/

    if (adtimes.size()!=0)
    {
        for (unsigned int b=0; b < adtimes.size()-2; b++)
        {
            /* make a list of the differences */
            diffadtimes.push_back(adtimes[b+1]-adtimes[b]);
        }

    std::vector<double> adstarts;

    /* find minimum time difference */
    std::vector<double>::iterator step = std::min_element(diffadtimes.begin(),diffadtimes.end());
    double minsteps = *step;

    for (unsigned int d=0; d< diffadtimes.size(); d++)
    {

        /* find all points in diff(adtimes) that change more than the minimum*/
        if (diffadtimes[d] > minsteps + 0.0001 )
        {
            /* store times */
            adstarts.push_back(adtimes[d+2]);
            /*                std::cout << adtimes[d+2] << "\n";*/
        }
    }

This block of code is concerned with finding the start of each afterdepolarisation. Simply put, it looks for discontinuities in the list of times, and stores them.

    std::ofstream outputfile;
    outputfile.open("/auto/users/bethmc/Data/LatestADs.dat");
    outputfile << "Time(s) membrane_voltage(mV) AD\n";
    for (unsigned int d=0; d < voltage.size(); d++)
    {
        outputfile << simtimes[d] << " " << voltage[d] << " ";

        /*output 1 if AD, 0 if not */
        bool found = 0;
        for (unsigned int e=0; e < adtimes.size(); e++)
        {
            if (simtimes[d] == adtimes[e])
            {
                found = 1;
                break;
            }
        }
        outputfile << found;

        outputfile << "\n";
    }

The output file contains columns of the time, the voltage, and whether or not an afterdepolarisation has been detected at that point.

    if (adstarts.size()>0)
    {
        return 1;
    }
    }
    return 0;
}

This function is called by other programs and used to find thresholds for interventions that cause afterdepolarisations. Hopefully, this code will be useful for finding out whether a drug that affects a particular ion channel in the heart will cause an arrhythmia.

Further to my last post, in which I attempt to form a vague understanding of Hodgkin and Huxley's giant squid axon model, I'm now looking at the gating mechanisms they used.

The opening, closing and inactivation of ion channels is vital for the characteristic shape of the action potential.

A) The sodium channels open and sodium floods into the cell: increases.
B) The potassium channels open, allowing potassium out of the cell: increases.
C) The sodium channels are inactivated when the membrane voltage is at its highest: .
D) The potassium channels close and the sodium channels are activated when the membrane voltage reaches its lowest: and increases.

This means that the sodium and potassium conductances vary in a complicated way with changes in the membrane voltage. The 'leak' current is simply directly proportional to the membrane voltage.

The changes in conductivity are modelled as "gates" for the sodium and potassium channels. The gates are represented by a dimensionless variable, which can be between 1 (fully active) and 0 (fully inactive). The rate of change of a gate with time is defined as:

where is the rate of movement of ions from outside to inside, and is the reverse.

Unlike for the rest of the model's features, the gating of the ion channels is not worked out from first principles. Instead, equations were fitted to match empirical data from experiments. Hodgkin & Huxley took measurements of each ionic current while keeping the membrane voltage constant, over a variety of different voltages, and used the data to find and expressions for each gate as functions of voltage.

For the potassium channel, there is only one type of gate, called the "n" gate. The permeability of the membrane to potassium varies with the 4th power of n (for equation fitting-ey reasons).

For the sodium channels, there are two types of gate. The gate being active encourages flow of sodium ions through the membrane, but the gate being active inactivates the sodium channels.