I deeply regret that I must begin this post by informing you that the entity in question is a giant axon from a squid, and not an axon from a giant squid. I can only imagine your disappointment on learning this fact - I recall that mine was considerable.
The models of heart cells that I'm working on at the moment are all based off a mathematical model from way back in 1952, created by Alan Hodgkin and Andrew Huxley. They described the electrical signal that passes down the axon of a squid's nerve cell when it is excited. The axon that controls the water jet propulsion system of a squid is particularly large, and easy to use in experiments.
The basis of this mathematical model is an understanding of the cellular features as components in an electrical circuit.* Just like in heart cells, the electrical signal is caused by the movement of charged particles, called ions, across the cell's outer membrane. The membrane of a neural cell acts like a capacitor, which means that ions accumulate on one side of the membrane, allowing it to store charge. This makes one side of the membrane more positive than the other side, leading to a voltage across the membrane.
This graph shows how the voltage across the membrane changes when the cell is stimulated.

The flow of ions across the membrane acts as an electrical current. Three types of ionic current are considered in this model: the sodium (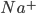 ) ions that flow into the cell and cause depolarisation of the membrane, the potassium (
) ions that flow into the cell and cause depolarisation of the membrane, the potassium (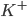 ) ions that flow out to repolarise the membrane, and the "leak" current (a mixture of ions, including chloride ions), which flows in both directions.
) ions that flow out to repolarise the membrane, and the "leak" current (a mixture of ions, including chloride ions), which flows in both directions.

The electrochemical gradients that power the flow of each type of ion are modelled as batteries, and the ion channels that permit ions to pass are represented by variable resistors.
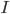 is the stimulus current that the cell receives from outside.
is the stimulus current that the cell receives from outside.
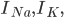 and
and 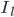 are the sodium, potassium and leak currents, respectively.
are the sodium, potassium and leak currents, respectively.
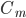 is the capacitance of the membrane (i.e. its ability to store charge)
is the capacitance of the membrane (i.e. its ability to store charge)
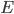 is the membrane voltage
is the membrane voltage
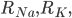 and
and 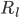 are the resistance of the membrane to letting each type of ion through
are the resistance of the membrane to letting each type of ion through
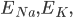 and
and 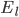 are the membrane potentials at which the flow of sodium, potassium or leak ions (respectively) through the membrane is zero.
are the membrane potentials at which the flow of sodium, potassium or leak ions (respectively) through the membrane is zero.
Since the current across the capacitor depends on the change in voltage over time and on the capacitance (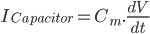 ), and the four components of the current (that are wired in parallel) all add up to the stimulus current (
), and the four components of the current (that are wired in parallel) all add up to the stimulus current (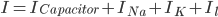 ), a unifying differential equation can be created.
), a unifying differential equation can be created.
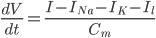
Where 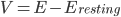 , i.e. the difference between the current membrane voltage and the usual, or "resting" voltage.
, i.e. the difference between the current membrane voltage and the usual, or "resting" voltage.
The next part of the paper deals with the gating mechanisms for the ion flows. My plan is to tackle that next week!
The original paper is available free from PubMed Central here. There's also a very good description of its content on Wikipedia, and an illustrated XML version of the model at the CellML model repository.
I put together some MATLAB code to solve the equations described in the paper - you can download and view or run the source code here.
One of the most interesting features of this paper are its descriptions of a possible mechanistic basis for the permeability of the cell membrane to ions. This paper was written long before ion channels were discovered and characterised in mammalian cells, so it's amazing how accurately it describes the action of the nerve cell. (A very readable account of the history of ion channels is available on Montana State University's webpage here, incidentally).
* which I'm sure is a helpful explanatory device for people who have the foggiest concept of how electricity works. I am not one of these people. I've relied on some A-level revision websites and my various physicist chums/siblings for that.